Support Vector Machine (SVM)

Overview

SVMs are a form of supervised learning. They learn from labeled data how the data groups can be optimally separated (classified) by hyperplanes in the data space. The SVM algorithm aims to find the optimal hyperplane (line, if 2D; plane, if 3D; hyperplane, if 3+D) such that the margin (or gap) between different classes is maximized (Figure 58). The algorithm assumes that the data belong to either a positive or negative set (i.e., binary classification). However, SVMs can still be used for problems that require distinguishing between more than two classes, by creating multiple classifiers. One approach is for each classifier to look at a different pair of classes in the problem (ex. "Class A" vs. "Class B", "Class B" vs. "Class C", "Class A" vs. "Class C"). Alternatively, the binary classification may also be implemented as one-versus-the rest (ex. "Class A" vs. "not Class A", "Class B" vs. "not Class B", etc.).

Once the model has been trained on a subset of data, it can then be used to similarly separate/classify unlabeled data. An unknown vector, u, is classified into either the positive or negative side of the found hyperplane through evaluation of the dot-product equation shown in Figure 59. The dot-product is crucial to SVM classification, as it allows for linear separation of data.

Because SVMs use hyperplanes for data classification, they are considered linear separators/classifiers. Nevertheless, SVMs can still be used in problems where the data are not linearly separable. In these situations, transforming the data into a higher dimension may allow for the classes to be separated with a hyperplane. However, these data transformations are computationally expensive. Using a non-linear kernel function essentially accomplishes this without the computational complexity of performing the transformation on the data first, and then taking the dot product. The kernel function is able to return the dot-product of the transformed data, allowing for non-linear separation of data. Two common non-linear kernel functions, polynomial and radial basis function, are shown in Figure 60. An example usage of the polynomial kernel transformation is shown in Figure 61.

Figure 61: Example of polynomial kernel with r=1 and d=2 transformation on two dimensional points a (1,2) and b (2,1). Through the transformation, the points are cast from two dimensions into six dimensions.

Figure 58: Illustration of SVM classification and margin maximization problem. In attempting to optimally separate the two data classes (green and purple points), the SVM algorithm finds the hyperplane (dotted red line) which maximizes the margin between the two classes (space between the two solid red lines). Data points which lie on the margin are called "support vectors."

Figure 59

Figure 60: Top - Equations for polynomal and radial basis function kernels. A and B are any two data points (vectors). In the polynomial kernal function, r is the polynomial coefficient and d is the degree. Bottom - Illustration of how different kernels may affect the data separation

Data Preparation

LINK TO SAMPLE OF THE DATA

LINK TO CODE

For a preview image of the raw data/starting point, please see FIGURE 16 on the Data Prep & Exploration tab of this website.

For this project, we will be using an SVM classifier to attempt to classify whether a song is "preferred" or "not preferred" by a user given a set of attributes from our acquired MSD and Spotify data. SVMs can only use numeric data attributes due to the algorithm using the dot product between vectors in the data space to both find the optimal hyperplane and classify new data vectors.

Creating the data labels/classes. The outcome variable for this classification problem will be called "Preferred" and will have a value of 1 for preferred, and 0 for not preferred. We will determine whether or not a song is preferred using the playcount information in our dataset. For each user, their mean playcount (from all of their listened-to songs) is calculated (Figure 62). For a given song which a user listened to, if the song playcount is over their mean playcount, then that song is labeled as "preferred" (1). Alternatively, it is labeled as "not preferred" (0). See Figure 63.

Cleaning & balancing the classes in the dataset. After labeling our data, we calculate the playcount variance within each user and remove users with a variance of less than 2. We have a large quantity of data (likely more than what we can realistically use in the SVM algorithm later), so doing this will help retain users with a wider range of playcounts and perhaps help our classification accuracy later. We then check the prevalence of each class in the dataset. In doing this, we find that there's about half as many "preferred" observations as there are "not preferred" observations. This imbalance should be corrected for, as the bias in our dataset will likely also bias our classifier. The data are sampled such that there are an equal number of observations from both classes.

Creating "preference distance" attributes. Before attempting classification, we create two more attributes which may assist with the preference classification task. Please refer back to the Introduction tab for an overview of how this quantitative metric was initially developed and utilized in prior works. In this project, we will be calculating "preference distance" a little differently. In prior works this metric was calculated within the context of the MUSIC five-factor model space. Due to time constraints with this project and the time-consuming nature of accurately translating our data into the MUSIC space, we will do an analogous calculation using some of the Spotify acoustic attributes instead of the MUSIC factors. The following attributes will be used from our dataset:

trackAcoustic: track "acousticness" score.
trackDanceable: track "danceability" score.
trackEnergy: track energy score.
trackInstrum: track "instrumentalness" score.
trackSpeech: track "speechiness" score.
trackVal: track overall valence measure.

I intentionally selected the high-level attributes from our dataset, to more closely parallel the high-level descriptive nature of the MUSIC factors and did not include the loudness or tempo attributes. Some of the other dataset attributes not mentioned here will still be used for the classification task (see below).

For each user, their mean for each of the attributes listed above is calculated (from all their listened-to songs). This gives us a 6-dimensional centroid for each user which can be taken to quantitatively represent their average listening habits on each of these six musical attributes (Figure 62). From there, a "preference distance" is calculated for each of a user's songs by taking the cosine similarity of the song's corresponding attribute values and their "centroid." This metric represents how similar a given song is on these six musical attributes to what that user has typically reported listening to.

In addition to the six-dimensional preference distance (which we also used in previous parts of this project) we will also calculate a three-dimensional preference distance designed with the Valence-Arousal-Depth model in mind. This preference distance is calculated in the same way, but only uses the trackVal, trackEnergy, and trackAcoustic attributes. WIth this, we will be able to compare the classifications using the two different preference distances. See Figure 63.

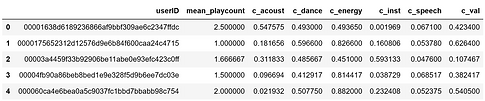
Figure 62: A temporary dataframe created to store mean attribute values for each user in our dataset. The mean_playcount variable is calculated from the playcounts for all of a user's songs. Mean playcount will be used later to create our dataset labels. Similarly, the six right-most columns of the dataset represent the mean acoutic attribute value for that user's data. These mean/center values for each user represent their average listening habits (in terms of musical characteristics) and will be used later to calculate the preference distance (similarity) metric.

Figure 63: This dataframe was created by merging the raw dataframe/starting point with the dataframe from Figure 62. The outcome variable "Preferred" can be seen on the right side. The dataframe was sampled such that both classes equally make up the data. The two preference distance attributes have also been added to the dataframe (right side).

Other attributes for training the model. So far the variables we have discussed in the context of our task are the outcome variable ("Preference") and the preference distance input variables ("pref_dist6" and "pref_dist3"). We will also use the following attributes directly from our original dataframe as inputs to the model:

artistPop: artist popularity score
trackPop: track popularity score

A preview of the final dataframe is shown below.

Split data into train / test subsets. Because SVM classifiers learn from labeled data, we need to train the model on a subset of labeled data and then test its performance on a separate, previously unseen subset of the data. We will use the common split proportion of 80% of our data for training, and 20% for testing. The rows of the dataframe (shown above) are shuffled/randomized. Then, the first 80% of the rows are saved as the training set, and the last 20% are saved as the testing set. This gives us two disjoint sets / data files. Sets that are not disjoint will misleadingly inflate the performance of the model. The full dataset, as well as the split train/test files can be found here. Figure 64 below shows a preview of the train and test sets.

Figure 64: Training set (top) and testing set (bottom) previews (first five rows of each).

SVM classifier with sigmoid kernel. In using this kernel function, I also tested various coefficients (0, 0.5, 1) in addition to the cost and gamma parameters. The model which only used the six-dimensional preference distance metric and the model which used both preference distance metrics tied for the best performance, both with a test accuracy score of 61%. The parameters for the former model were a cost of 1, gamma of 0.16, and coefficient of 1, and the parameters for the latter were a cost of 10, gamma of 0.16, and coefficient of 0.5. The confusion matrix for the test data classification of both is shown below. The first model has slightly higher precision (66% vs. 64.8%) while the second model has slightly higher recall (63.6% vs. 60%). The second model has the highest F1 score (0.641 vs 0.628). A plot of the SVM classification for this model is shown below. The performance of this classifier with the sigmoid kernel exceeds that of the other two kernels tested.

Results

All of the following SVM classifiers are created using the svm function from the e1071 library in R. I tried three different kernel functions: linear, radial basis function, and sigmoid. For each kernel function, I tried three different classification models:

Preferred ~ artistPop + trackPop + pref_dist6
Preferred ~ artistPop + trackPop + pref_dist3
Preferred ~ artistPop + trackPop + pref_dist6 + pref_dist3

For each kernel function and model, I also tried various cost values: 0.001, 0.1, 1, 10, 50.

Code is available here.

SVM classifier with linear kernel. For the linear kernel SVM, the model which used both preference distance metrics together had the best performance, with a cost of 0.1 resulting in the highest test accuracy score of 59%. The confusion matrix for the test data classification is shown below. The classifier is more successful at predicting not preferred songs than preferred songs. The model which used the six-dimensional preference distance metric only had the second-best performance, with a cost of 0.1 giving a test accuracy of 55%.

SVM classifier with RBF kernel. In using this kernel function, I also tested different values of the gamma parameter (0.16, 0.33, 0.49) in addition to the cost parameters. The model which only used the six-dimensional preference distance metric had the best performance, with a cost of 1 and gamma of 0.16 resulting in the highest test accuracy score of 54%. The confusion matrix for the test data classification is shown below. Again, the classifier is more successful at predicting not preferred songs. However, compared to the linear kernel SVM, this classifier is much worse at predicting preferred songs. The performance does not exceed that of the SVM with linear kernel. The model which used both preference distance metrics together had the second-best performance, with a cost of 1 and gamma of 0.16 giving a test accuracy of 52%.

Conclusions

In this section, we used SVMs to attempt to classify user preferred and not-preferred songs. We experimented using three different kernel functions for the classifier, as well as two different ways of calculating how similar a given song was to what that user typically listened to. We achieved the highest prediction accuracies when using the six-dimensional preference distance metric, or when using both the six-dimensional metric and the three-dimensional metric together. It's important to reiterate that the preference distances calculated here do not exactly reflect previously studied models/dimensions of musical preference, due to time constraints and the attributes given in the data. Nevertheless, the result supports the theory that more than three dimensions assist in capturing user preference. The higher performance of the model when using both distances together suggests that perhaps some dimensions of the preference distance may be more significant, or correlated to the preference labels, than others. Future work may investigate the roles that each of the dimensions/attributes play individually, and perhaps consider a "weighted" preference distance.